In the last couple of years, my girlfriend sprained her ankle multiple times. A month ago, a ligament in her angle started to get frequently dislocated. She has to locate it back manually, a couple of times per day. Ouch.
She decided to try Kinesio tape to improve her condition. Since she sometimes forgets to put it on, that’s an opportunity to evaluate whether the tape works; decreases the number of dislocations per day.
We will use Bayesian Poisson regression to tackle the problem. Why Poisson?
If the number of trials
nis very large (and usually unknown) and the probability of a successpis very small, then a binomial distribution converges to a Poisson distribution with an expected rate of events per unit time of \(\lambda = np\). - Statistical Rethinking by Richard McElreath
So, during the day, there are a lot of opportunities (trials) for dislocations, but dislocations (successes) happen rarely.
Data
Here’s the data I collected:
library(tidyverse)
library(rethinking)
library(tidybayes.rethinking)
library(tidybayes)
library(bayesplot)
df <- tribble(
~date, ~dislocations, ~tape, ~hours,
1, 5, 0, 12,
2, 4, 0, 12,
3, 3, 0, 12,
4, 1, 1, 12,
5, 0, 1, 12,
6, 1, 0, 12,
7, 3, 0, 12,
8, 2, 0, 12,
9, 0, 1, 12,
10, 1, 1, 8,
10, 1, 0, 4,
11, 0, 1, 12,
12, 1, 1, 12,
13, 1, 0, 2,
13, 2, 1, 10
) |>
mutate(
across(.fns = as.integer),
day = hours / 12
)
The data represents dislocation counts per date (the actual date is
not important so it’s just an integer). I assumed there are twelve
active hours per date. Because sometimes she used the tape for a couple
of hours, there can be multiple rows per date with the number of hours
that sum up to twelve. Dummy variable tape denotes whether
she used the tape. Based on the hours I calculated the
portion of the day.
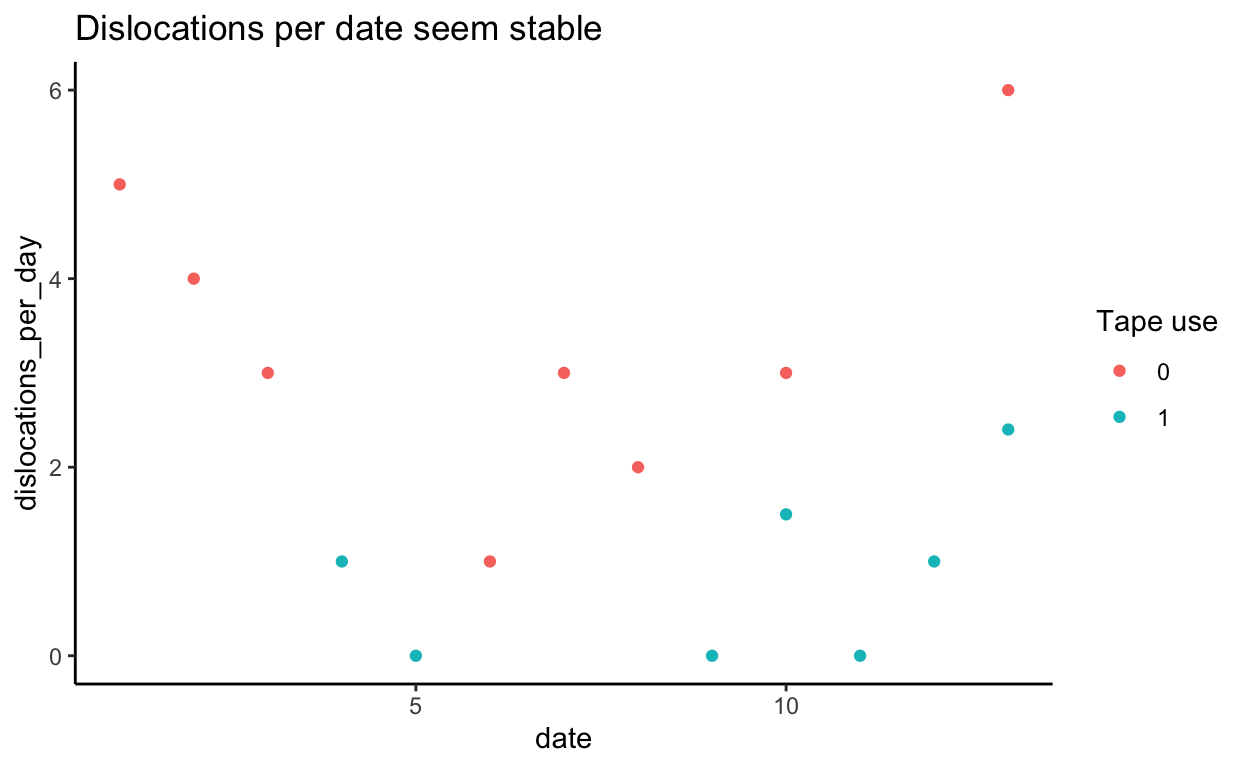
From the plot below we can see there’s no trend in the number of dislocations.
df |>
mutate(dislocations_per_day = dislocations / day) |>
ggplot(aes(date, dislocations_per_day, color = as.factor(tape))) +
geom_point() +
labs(title = "Dislocations per date seem stable", color = "Tape use")
Modeling
Our assumptions:
- she uses the tape randomly1 and doesn’t change her behavior once she wears it;
- the dislocations are independent of one another;
- the average rate at which events occur is constant.
There’s no placebo in our experiment, so a placebo might account for potential improvements. However, there are no side effects of using the tape (besides monetary) so we are fine even if the improvement would be due to placebo.
The system can be described using the following formulas:
\[ dislocations_i \sim Poisson(\lambda_i) \\ log(\lambda_i) = log(day_i) + a + b * tape_i \\ a \sim \mathcal{N}(0.5, 1) \\ b \sim \mathcal{N}(0,1) \\ \]
Daily \(dislocations\) follow the
Poisson distribution with parameter \(\lambda\). \(log(\lambda)\) is calculated as a linear
combination of log(day) that presents a duration, parameter
a, rate of dislocations without the tape, and parameter
b that represents the increase in rate due to the use of
the tape. Since we have number of dislocations per different time
durations, not only per day, we include the \(log(day_i)\) term. This makes sense because
we are interested in the rate of dislocations per day (represented by
twelve active hours):
\[\frac{\lambda_i}{day_i}=exp(a + b * tape_i)\] If we \(log\) and apply \(log(a/b) = log(a) - log(b)\) on both sides, we get:
\[log(\lambda_i) - log(day_i) = a + b*tape_i\] Now we only need to move \(-log(day_i)\) to the right side. Voila!
We rewrite the same set of formulas to STAN using the rethinking package:
We’ll also calculate the ratio between dislocation rates
of taped and non-taped ankle.
By calling summary we can see that b has a
negative value, denoting that the tape helps. Similarly,
ratio tells us that dislocations happen around third the
usual rate when the tape is used.
precis(m)
mean sd 5.5% 94.5% n_eff Rhat4
a 1.0070880 0.2266219 0.6429809 1.360209 1219.078 1.001280
b -1.1253477 0.4301082 -1.8359004 -0.462828 1501.478 1.000527
ratio 0.3550894 0.1528327 0.1594699 0.629501 1480.858 1.000277We would have to exponentiate the values of a and
b to get the actual dislocation rates. Below, we’ll plot
the posterior distribution of ratio that is calculated as \(ratio =
\frac{e^{a+b}}{e^a}=\frac{\lambda_{tape}}{\lambda_{no
tape}}\)
posterior_ratio <- spread_draws(m, ratio)
ggplot(posterior_ratio, aes(ratio, fill = stat(abs(x) < 0.5))) +
stat_halfeye() +
labs(title = "Dislocation rate decreases for a factor of 3 when using the tape")
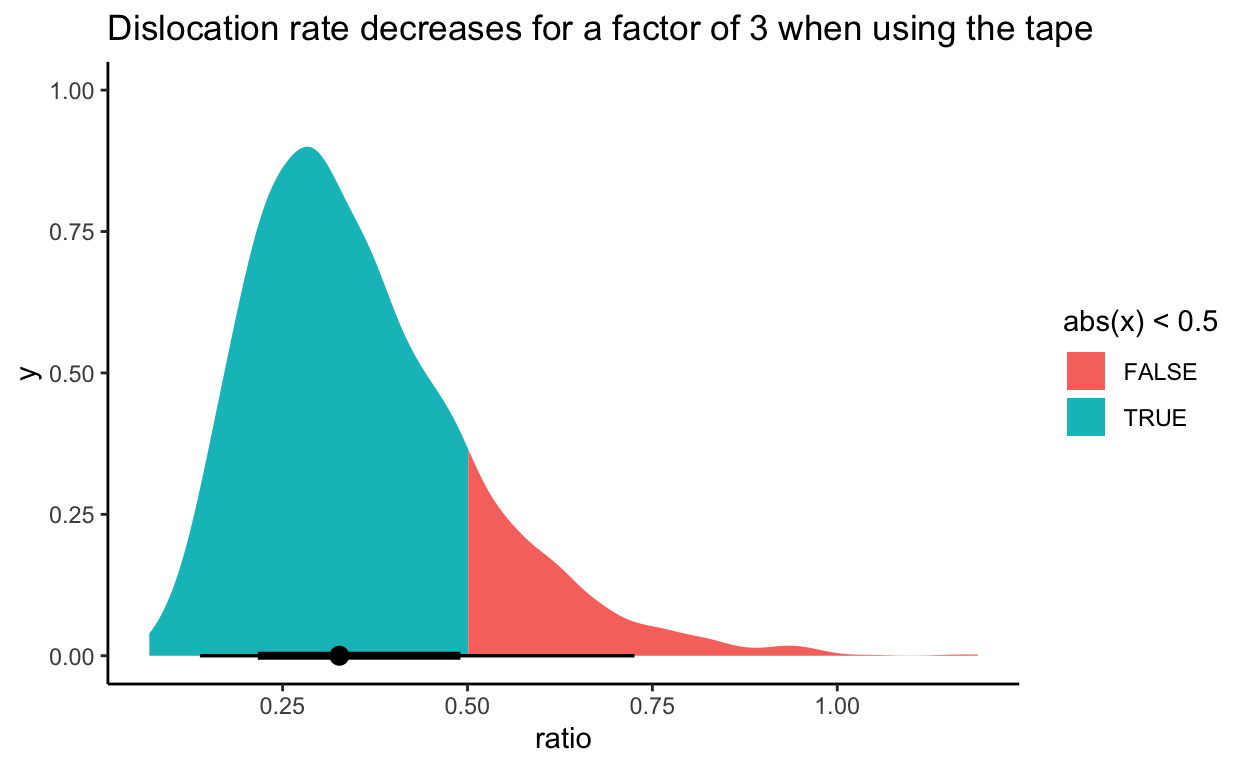
Bayesian approach enables us is to make probability statements about
the posterior distributions. For example, we can calculate probability
that ratio is lower than 0.5 (integral of blue area on the
plot above):
# A tibble: 1 × 1
prob_less_than_0.5
<dbl>
1 0.844Let’s also do a posterior predictive check - simulating replicated data under the fitted model and comparing these to the observed data2. This tells us whether the model gives “valid” predictions about reality.
dislocations_rep <- predicted_draws(object = m, newdata = d, ndraws = 50) |>
ungroup() |>
pivot_wider(id_cols = .draw, names_from = .row, values_from = .prediction) |>
select(-.draw) |>
as.matrix()
ppc_dens_overlay_grouped(
d$dislocations,
dislocations_rep,
group = if_else(d$tape > 0, "tape", "no tape")
) +
labs(title = "Comparison of empirical data distributions")
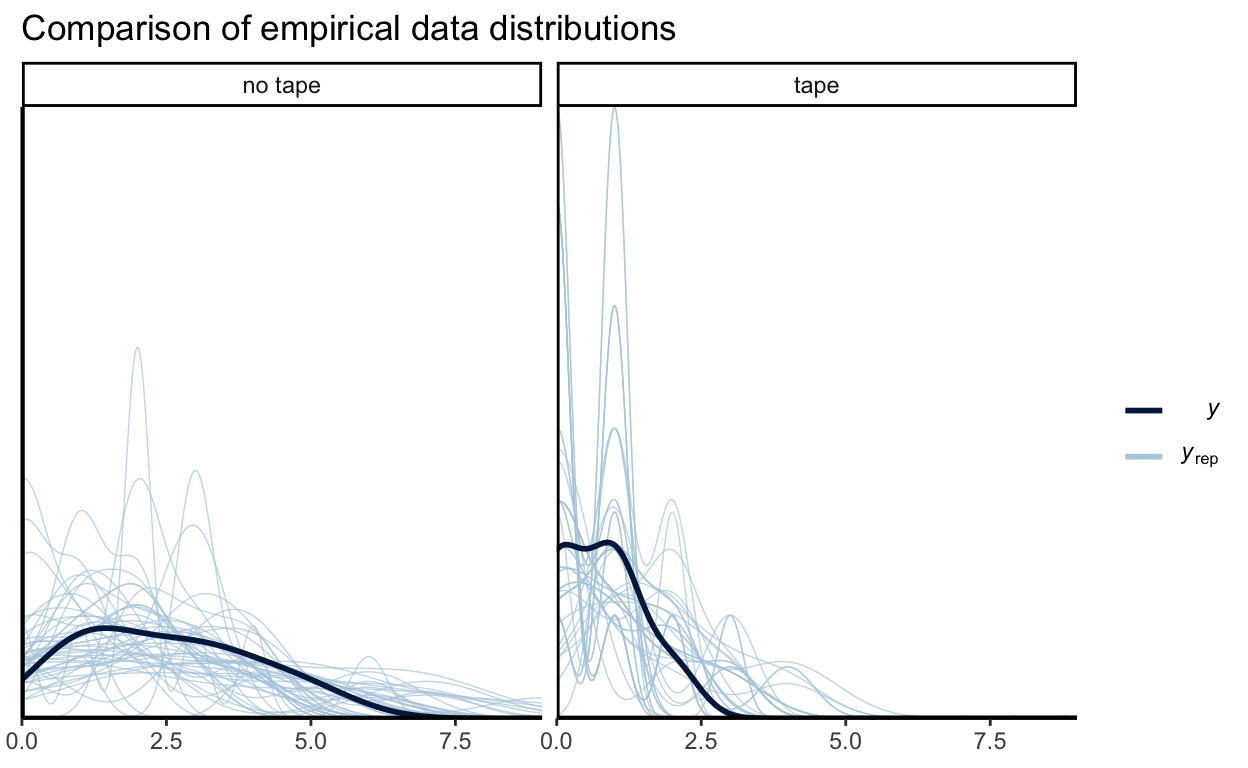
We can see that true data has shorter tails compared to the simulated ones. This can be due to my girlfriend changing her behavior after multiple dislocations.
From now on, she uses Kinesio tape every day. I’m kidding. Writing this blog post took me so long that her condition improved by itself. Time works even better than Kinesio tape.
She could flip a coin in the morning and wear a tape based on the outcome.↩︎