Some time ago I was watching Smoking: The Dataset series of videos on calmcode.io. They show you how to analyze and compare 10-year mortality rates of smokers vs non-smokers. ¹

In this post, I’ll use Bayesian inference together with a generalized linear model, to calculate the effect of being a smoker compared to the visual approach from calmcode. First, let’s see what they figured out.

Visual approach

Each row in the smoking dataset represents a person, whether she smokes and is still alive after ten years.

library(tidyverse)
library(rethinking)
library(tidybayes.rethinking)
library(tidybayes)

df_raw <- readr::read_csv("smoking.csv", col_types = "cfi")

df <- df_raw %>% 
  transmute(
    age,
    is_smoker = smoker,
    is_dead = if_else(outcome == "Dead", 1L, 0L)
  )

head(df_raw)

# A tibble: 6 × 3
  outcome smoker   age
  <chr>   <fct>  <int>
1 Alive   Yes       23
2 Alive   Yes       18
3 Dead    Yes       71
4 Alive   No        67
5 Alive   No        64
6 Alive   Yes       38

We also tweaked the dataset a bit and saved it to df. This will come in handy later on. From now, we will focus on mortality instead of survival rates.

The most basic (and naive) approach would be just to calculate mortality rates per smoking status.

df %>% 
  group_by(is_smoker) %>% 
  summarise(death_rate = mean(is_dead))

# A tibble: 2 × 2
  is_smoker death_rate
  <fct>          <dbl>
1 Yes            0.239
2 No             0.314

Wow, it seems that smokers have lower mortality rates! But… we don’t “control” for age. Let’s compare mortality rates per age group:

df_agg <- df %>% 
  mutate(round_age = plyr::round_any(age, 10)) %>% 
  group_by(round_age, is_smoker) %>% 
  summarise(death_rate = mean(is_dead), .groups = "drop")

ggplot(df_agg, aes(round_age, death_rate, color = is_smoker)) + 
  geom_line() + 
  labs(
    title = "Mortality rates of smokers are higher for all age groups",
    y = "10-year mortality rate",
    x = "Age group"
  )

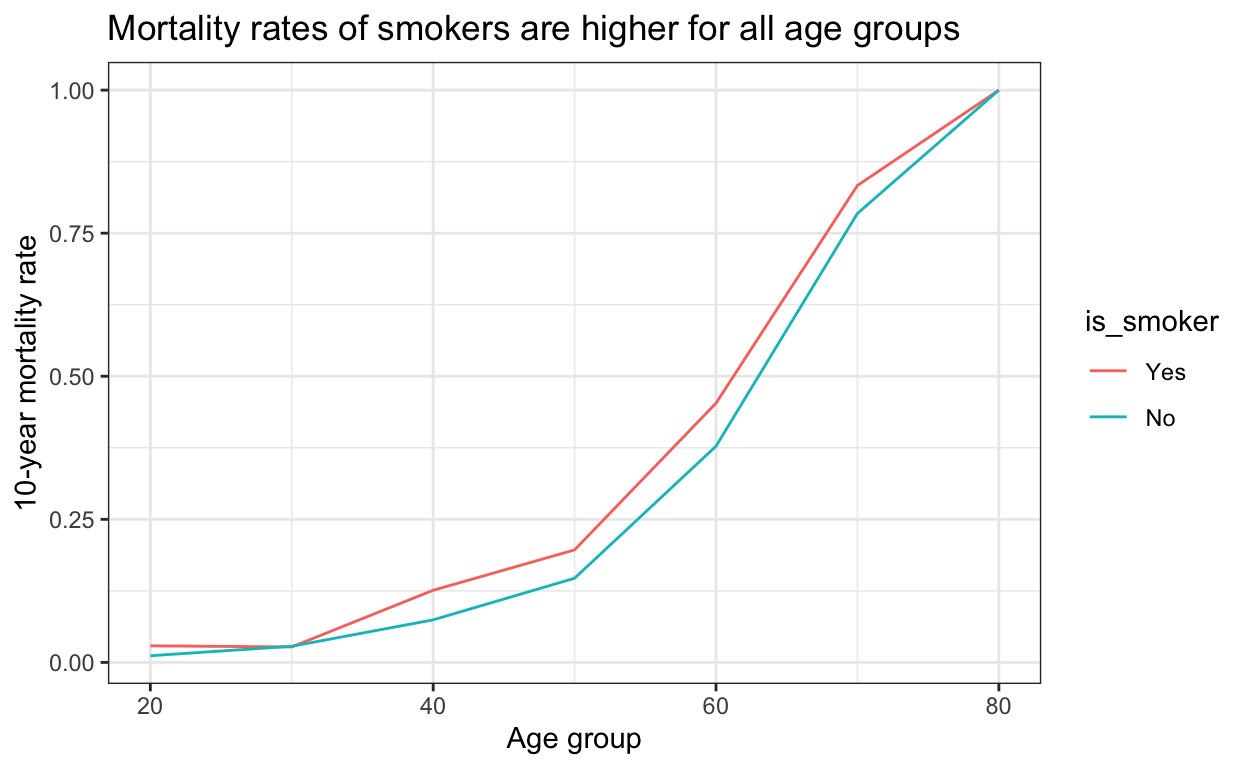
This shows a completely different picture! Smokers have higher mortality rates across all age groups. Before, we got different aggregated results because of different age proportions between smokers and non-smokers represented in the dataset. That’s known as Simpson’s paradox.

Calmcode videos stop at this conclusion. But I was wondering how to estimate the difference more precisely, without binning the ages? Bayes to the rescue.

Bayesian approach

We’ll use a generalized linear model with binomial likelihood. When - as in our case - the data is organized into single-trial cases (whether the person died in the next 10 years), the common name for this model is logistic regression. We’ll use logit link to model the relationship between age and mortality rate. This transformation is necessary in order to take care that all p values map from \([- \infty, \infty]\) to [0,1] - otherwise we would have to be careful when defining the priors.

So, here’s how logit(p) ~ age looks on a plot:

ggplot(df_agg, aes(round_age, logit(death_rate), color = is_smoker)) + 
  geom_line() + 
  labs(
    title = "We will approximate logit(p) ~ age with linear function.", 
    y = "logit(10-year mortality rate)", 
    x = "Age group"
  )

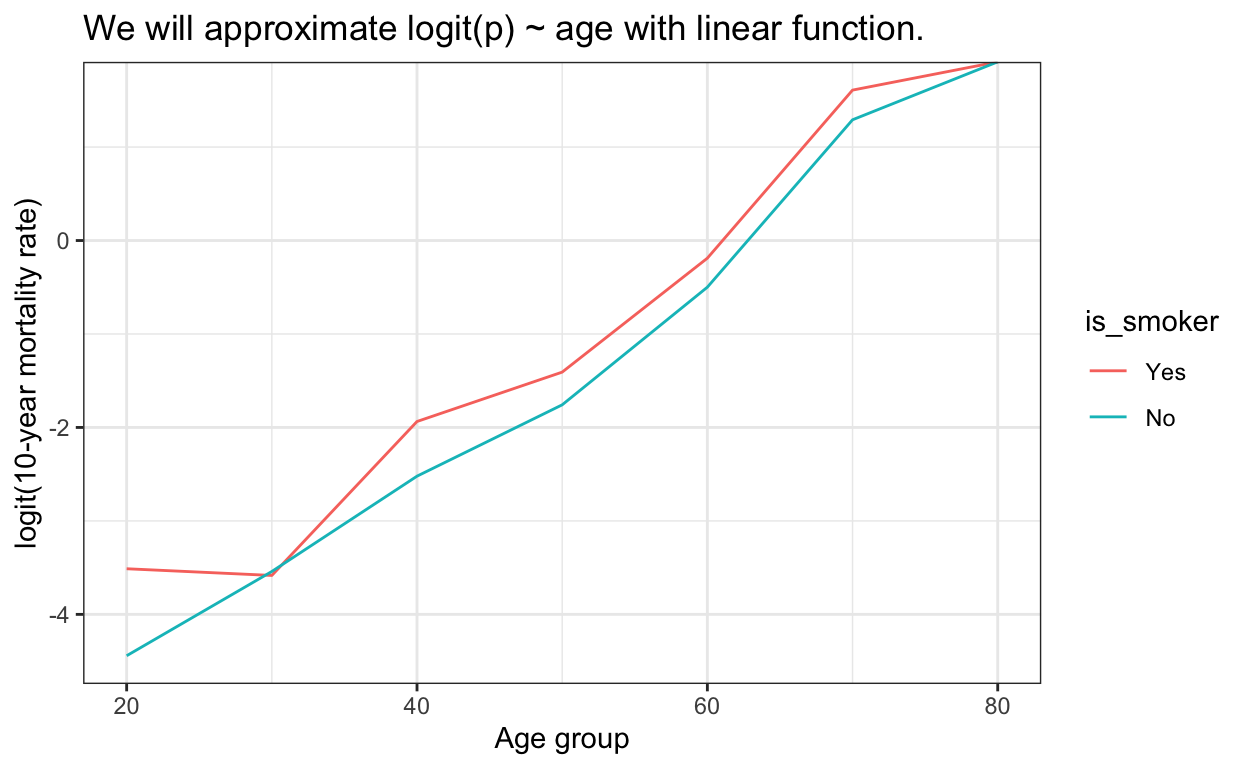
By eyeballing the plot it seems that we can model both logit(death_rate) as a linear combination of mortality rate at some age (intercept) and slope that represents how mortality rate is changing with age. It also seems that the slope is the same for both groups.

From this, we can construct a list of formulas for our model and run it:

formulas <- alist(
    is_dead ~ dbinom(1, p),
    logit(p) <- a[is_smoker] + b * (age - 60),
    a[is_smoker] ~ dnorm(-0.3, 0.25),
    b ~ dnorm(0.1, 0.05)
)

model <- ulam(formulas, data = df, warmup = 200, iter = 500, chains = 4, cores = 4)

Let me explain the formulas:

is_dead follows Binomial distribution with 1 trial (also known as Bernoulli distribution) and \(p\) represents a probability of success (in our case success equals death in the next 10 years).
Link function logit(p) is a linear combination of a ten-year mortality rate at age sixty that depends on whether a person smokes, denoted by the intercept a, and slope b that is shared among smokers and non-smokers. I decided to use such model based on the plot above. logit(death_rate) seems to be linearly correlated with age. The slope seems to be the same for both groups. The only thing that is different is the intercept. I decided to calculate it at age 60 instead of 0 because
- it’s more intuitive;
- the model doesn’t make sense for low ages.
Prior for the intercept a that represents mortality rate at age sixty is the same for both groups. It’s based on eyeballing but it is wide enough and in the limits of what makes sense. ²
Slope’s prior b is also based on eyeballing but again could be determined in advance from online datasets and in ideal scenario stricter.

Before looking at the model, let’s double-check the priors:

prior <- extract.prior(model, n = 200)

tibble(
  sample = 1:200,
  a = prior$a[,1], # you get two priors for intercepts (one for each group) but they are the same
  b = prior$b
) %>%
  tidyr::crossing(age = min(df$age):max(df$age)) %>%
  mutate(p = pmap_dbl(list(a, b, age), \(a, b, age) inv_logit(a + b * (age - 60)))) %>%
  ggplot() +
  geom_line(aes(age, p, group = sample), alpha = 0.2) +
  geom_point(data = df_agg, aes(round_age, death_rate, color = is_smoker)) + 
  labs(title = "Priors seem fine", y = "10-year mortality rate")

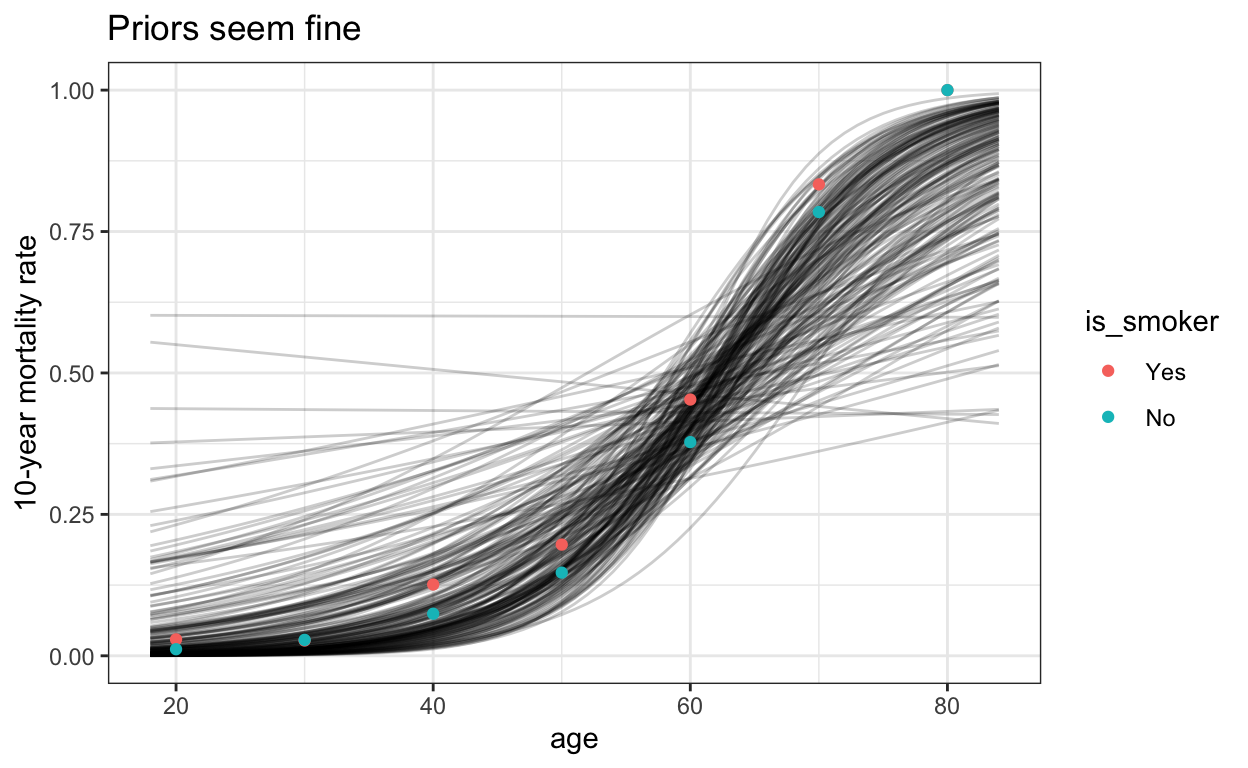
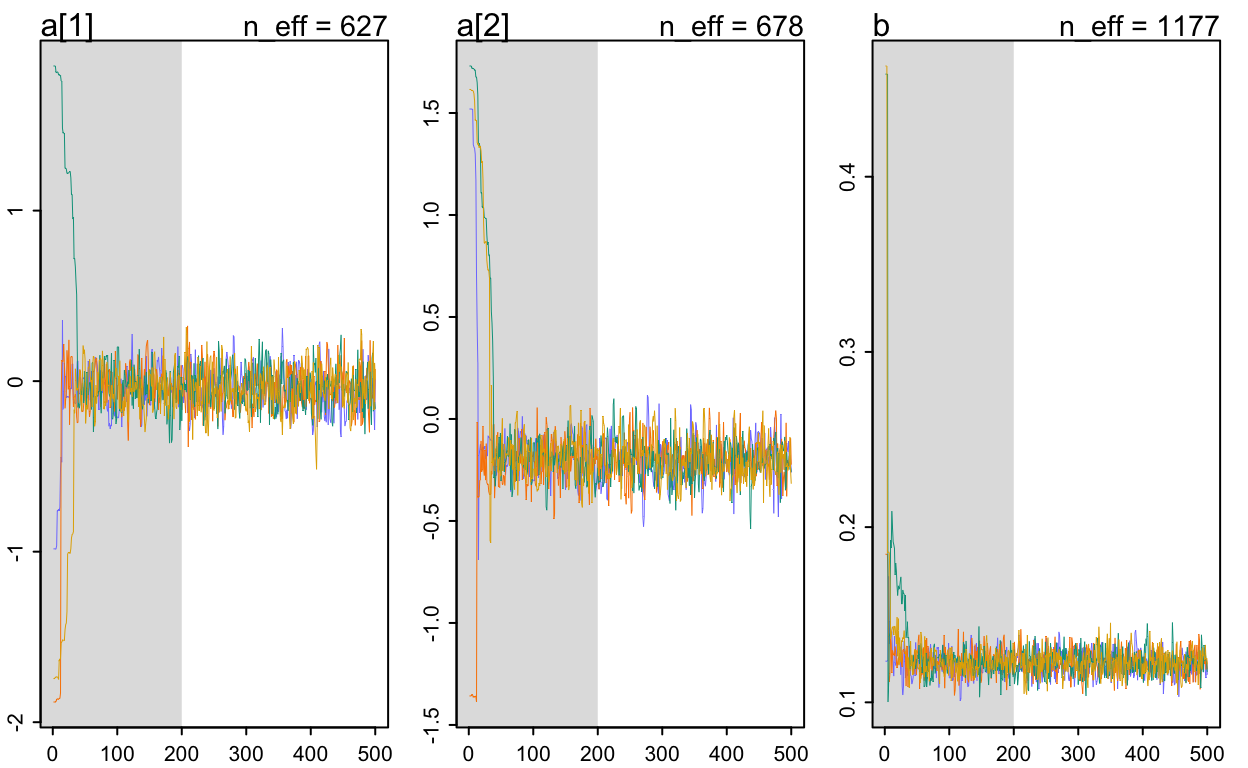
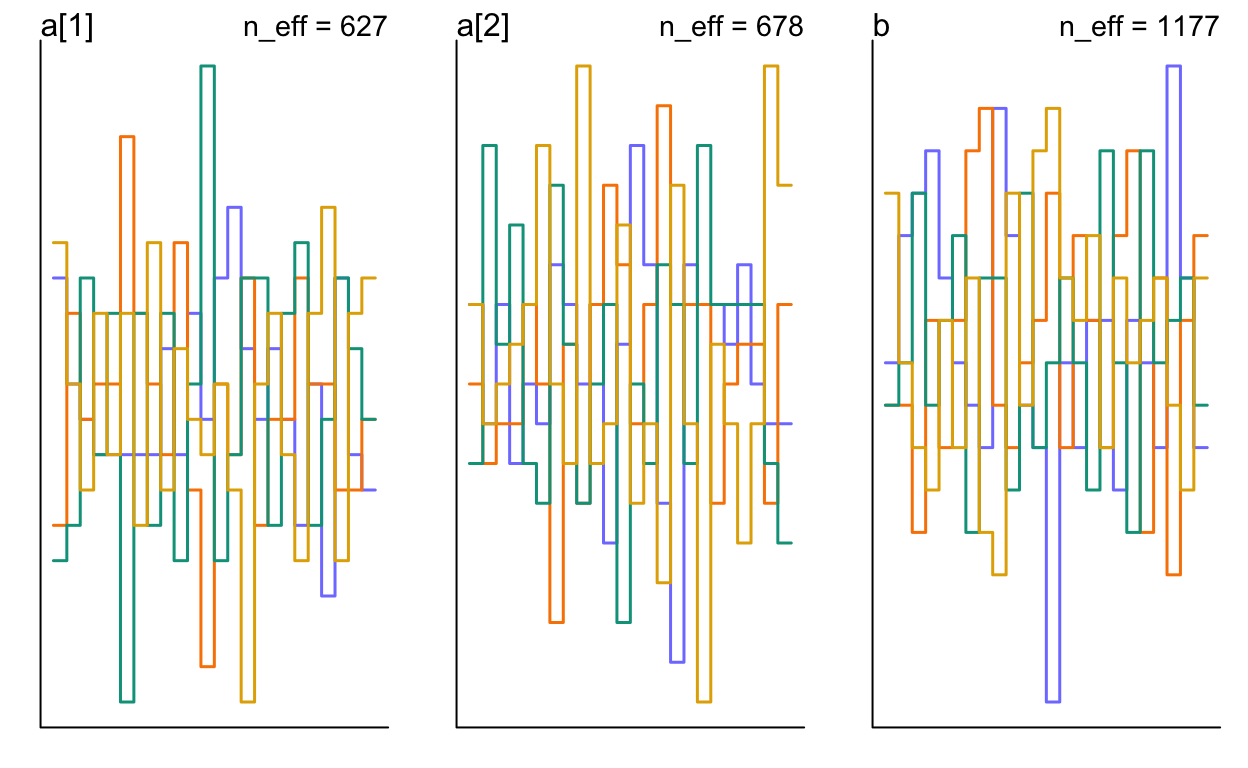
Priors seem fine - informative enough but also flexible. Trace and trank plots of chains also look good!

Take a look at trace and trank plots.

traceplot(model)

[1] 500
[1] 1
[1] 500

trankplot(model)

Here’s the summary of the model:

summary(model)

Inference for Stan model: 49f5d62bf6172f02e3638f3ae2372250.
4 chains, each with iter=500; warmup=200; thin=1; 
post-warmup draws per chain=300, total post-warmup draws=1200.

        mean se_mean   sd    2.5%     25%     50%     75%   97.5%
a[1]   -0.04    0.00 0.12   -0.26   -0.13   -0.05    0.04    0.20
a[2]   -0.20    0.00 0.10   -0.39   -0.26   -0.20   -0.14    0.01
b       0.12    0.00 0.01    0.11    0.12    0.12    0.13    0.14
lp__ -474.88    0.06 1.23 -478.10 -475.46 -474.57 -473.98 -473.49
     n_eff Rhat
a[1]   627    1
a[2]   678    1
b     1177    1
lp__   494    1

Samples were drawn using NUTS(diag_e) at Mon Jan 10 19:35:02 2022.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

We can see that the intercept of smokers, represented by a[1] has a higher mortality rate compared to the intercept of non-smokers a[2]. We can plot the whole distributions for both parameters (already converted into mortality rates at age 60) and their difference using handy functions from tidybayes package: ³

samples_a <- model %>%
  recover_types(df) %>%
  spread_draws(a[is_smoker]) %>% 
  mutate(p = inv_logit(a)) %>% 
  bind_rows(.,  compare_levels(., p, by = is_smoker)) 

ggplot(samples_a, aes(p, is_smoker)) + 
  stat_halfeye() + 
  labs(title = "Posterior distributions for intercepts and their difference")

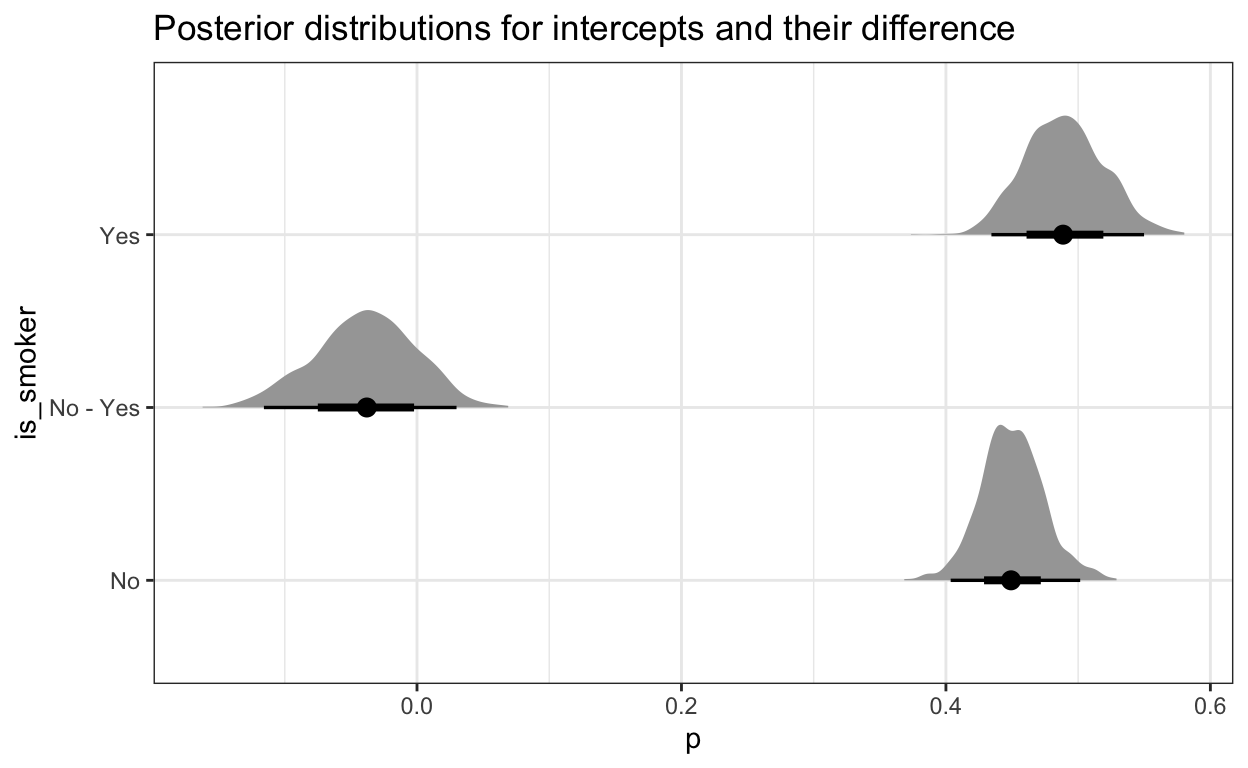
These distributions are based on the posterior samples. With them, we can also calculate the probability that non-smokers have lower mortality rate:

samples_a %>% 
  filter(is_smoker == "No - Yes") %>% 
  summarise(prob = mean(p < 0))

# A tibble: 1 × 2
  is_smoker  prob
  <chr>     <dbl>
1 No - Yes  0.845

There’s around 85% chance that smokers have a higher mortality rate. We can also visualize how the difference in mortality rate is changing with age (note that the shape of the difference was defined by our model - but not the magnitude):

newdata <- tidyr::crossing(
  age = 20:90, 
  is_smoker = unique(df$is_smoker)
)

linpreds <- add_linpred_draws(model, newdata = newdata, value = "p") 

linpreds %>% 
  group_by(age, .draw) %>% 
  summarise(
    p_diff = p[is_smoker == "Yes"] - p[is_smoker == "No"]
  ) %>% 
  ggplot(aes(x = age)) +
  stat_lineribbon(aes(y = p_diff), .width = 0.9, fill = "gray") + 
  labs(
    title = "Mean difference in mortality rate with 90% credible interval" ,
    subtitle = "Shape of the difference was imposed by our model.",
    y = "Difference in 10-year mortality rate with 90% CI"
  )

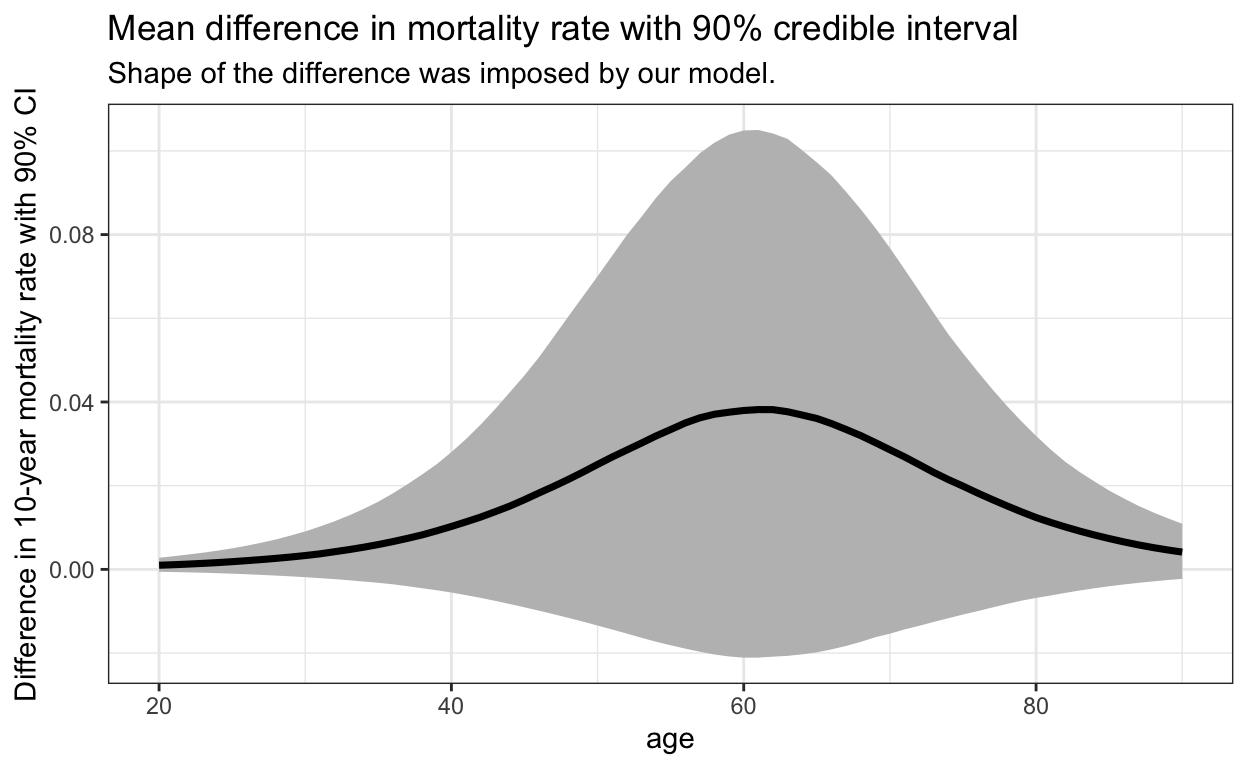
There seems to be up to ~4% mean increase (90% credible intervals are between 10% and -2.5%) in the 10-year mortality rate for around age 60 which shrinks for younger and older. This might make sense:

for younger, the effects of smoking are not as big yet (and they have way smaller mortality rates anyway);
older people are more likely to die even without smoking.

We could calculate the relative uplift of mortality by dividing instead of subtracting mortality rates. In this case, relative uplift is around almost 20% for younger and then starts slowly dropping, becoming around 10% at age 60, and then almost negligible.

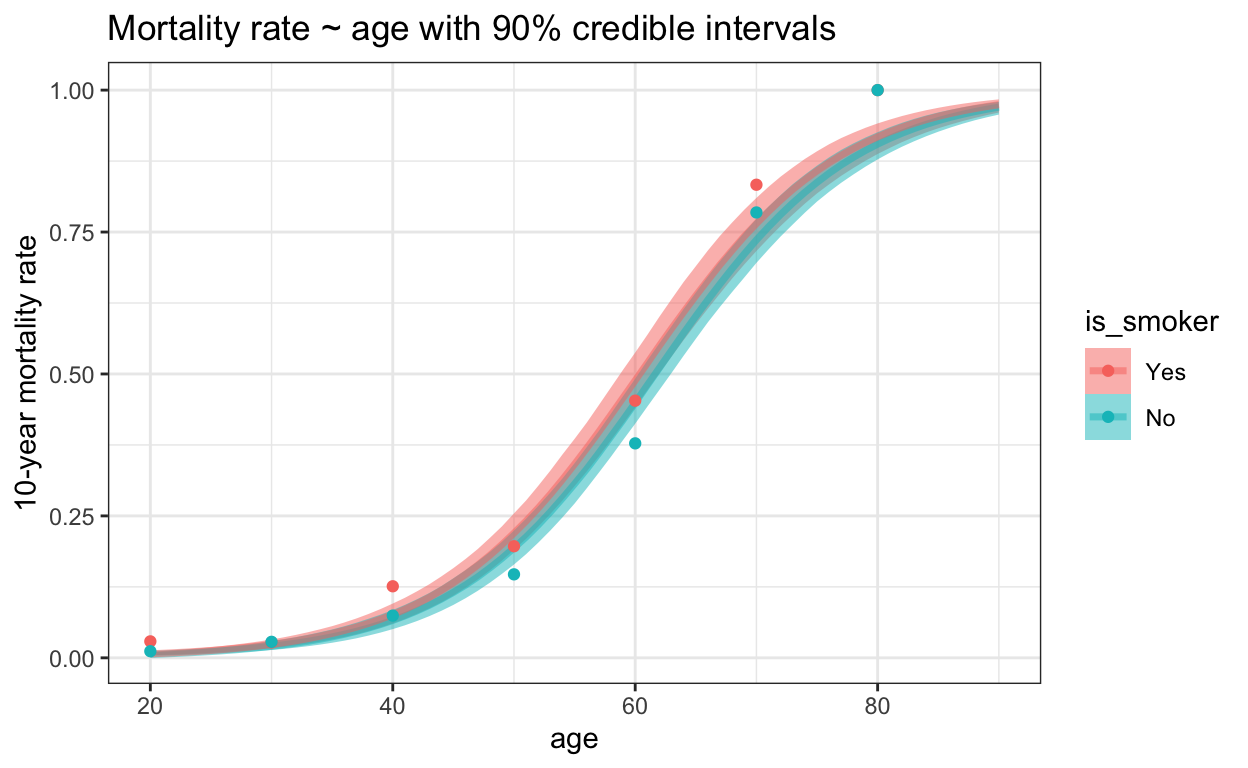
We can also visualize mortality rates with 90% credible intervals for both groups across all ages:

ggplot(linpreds, aes(x = age, color = is_smoker, fill = is_smoker)) +
  stat_lineribbon(aes(y = p), .width = 0.9, alpha = 0.5) +
  geom_point(data = df_agg, aes(x = round_age, y = death_rate)) + 
  labs(
    title = "Mortality rate ~ age with 90% credible intervals",
    y = "10-year mortality rate"
  )

So… don’t smoke. And use smokin’ Bayes.

Beware, not the effect of smoking - but being a smoker - because lifestyles of people who smoke from those who don’t differ in other aspects besides smoking.↩︎
I could also reuse it from some other online datasets.↩︎
This vignette contains the most common use cases.↩︎

Smokin’ Bayes

Visual approach

Bayesian approach